Question

The weight (W kg) of a decaying radio active substance after n years is given by W= Wo(1/2)^n/100, where Wo kg is the initial weight of the substance. 1. Atleast how many years will it take for the radioactive substance to lose to 10% of its initial weight?

Answer 1

332.19 years

Explanation:

The weight, W of the substance after n years is given by:

`W=W_o\mleft((1)/(2)\mright)^{(n)/(100)}`

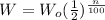
Let the initial weight = 100%

If the substance loses to 10% of its initial weight, then:

• Wo = 100%

,

• W= 10%

Substitute these into the formula:

`\begin{gathered} (10)/(100)=(100)/(100)\mleft((1)/(2)\mright)^{(n)/(100)} \\ \implies0.1=\mleft((1)/(2)\mright)^{(n)/(100)} \end{gathered}`

We then solve the equation for the value of n.

Take the logarithm of both sides.

`\begin{gathered} \log (0.1)=\log \mleft((1)/(2)\mright)^{(n)/(100)} \\ \implies\log (0.1)=(n)/(100)\log ((1)/(2))^{} \end{gathered}`

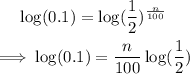
Then divide both sides by log(1/2):

`\begin{gathered} (\log (0.1))/(\log ((1)/(2)))=\frac{(n)/(100)\log((1)/(2))^{}}{\log((1)/(2))} \\ \implies(n)/(100)=(\log (0.1))/(\log ((1)/(2))) \end{gathered}`

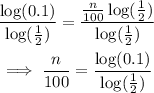
Finally, multiply both sides by 100:

`\begin{gathered} 100*(n)/(100)=100*(\log (0.1))/(\log ((1)/(2))) \\ n=332.19\text{ years} \end{gathered}`

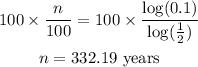
It will take at least 332.19 years for the radioactive substance to lose to 10% of its initial weight.