Given:
Two intergers have a sum of 47 and a difference of 23.
Let's find the product of the two numbers.
Let x and y represent the numbers.
We have:
Two integers have a sum of 47: x + y = 47
Two integers have a difference of 23: x - y = 23
We gave the system of equations:
x + y = 47.......................equation 1
x - y = 23.......................equation 2
Let's solve the system simultaneously using substitution method.
Rewrite equation 1 for x:
x = 47 - y
Substitute (47 - y) for x in equation 2:
(47 - y) - y = 23
47 - y - y = 23
47 - 2y = 23
Subtract 47 from both sides:
47 - 47 - 2y = 23 - 47
-2y = -24
Divide both sides of the equation by -2:
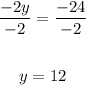
Now, substitute 12 for y in either of the equations.
Let's take equation 1.
x + y = 47
x + 12 = 47
Subtract 12 from both sides:
x + 12 - 12 = 47 - 12
x = 35
Therefore, we have:
x = 35, y = 12
The numbers are 35 and 12.
To find the product of the numbers, let's multiply the numbers:
35 x 12 = 420
Therefore, the product of the numbers is 420.
ANSWER:
420