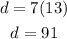We need to find an equation that describes the relationship between days and week.
We know that one week has 7 days:
So, to find the number of days for a given number of weeks, what we need to do is multiply the number of weeks by 7.
If we call the number of weeks "w" and the number of days "d", the equation that describes the proportional relationship is:
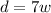
The number of days is equal to the number of weeks multiplied by 7.
Now with this, we can complete the table of values. For 4 weeks, the number of days is:
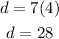
For 5 weeks, the number of days is:
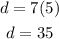
To complete the next row, we don't need the days, we need the number of weeks. For that, we take our equation and substitute the number of days:
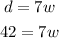
And we solve for "w" by dividing both sides by 7:
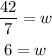
Finally, for the last row, we find the number of days in 13 weeks using our equation: