Question

Find two solutions for the equation 4x+3y=24 , draw it's graph .

Answer 1

The equation of consideration is:

`4x\text{ + 3y = 24}`

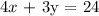
Since two unknowns ( x and y) are given in just one equation, to get each set of the solutions, we are going to choose a value of x and get a corresponding value of y

Let x = 0, to get the value of y at point x = 0, substitute this value of x into the given equation:

`4(0)\text{ + 3y = 24}`
`3y\text{ = 24}`
`y\text{ = }(24)/(3)\text{ = 8}`

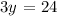
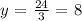
The first set of solutions is therefore:

`x\text{ = 0, y = 8}`

To get the second set of solution, let us choose x = 3 and substitute this value into the given equation:

`4(3)\text{ + 3y = 24}`
`12\text{ + 3y = 24; 3y = 24 - 12; 3y = }12;\text{ y = 12/3; y = 4}`

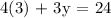
The second set of equation is:

`x\text{ = 3, y = 4}`

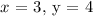
The above is the graph showing the two sets of solutions