Question

Show that when -9p2 + 4p + 1970 = 0, Total Revenue is at its maximum.Find the price and quantity which maximise Total Revenue.

Answer 1

Step 1

Write the demand function equation

`Q=-9p^2+4p\text{ + 1970}`

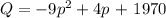
Step 2:

To find the price and quantity which maximize the revenue

You will find the derivative of Q with respect to price

`\begin{gathered} (dQ)/(dp)\text{ = -18p + 4} \\ -18p\text{ + 4 = 0} \\ 18p\text{ = 4} \\ p\text{ = }(4)/(18)\text{ = }(2)/(9) \end{gathered}`

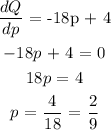
Step 3:

Find the quantity demand by substituting p = 2/9

`\begin{gathered} Q\text{ = -9 }*\text{ (}(2)/(9))^2\text{ + 4 }*\text{ }(2)/(9)\text{ + 1970} \\ =\text{ -0.44 + 0.888 + 1970} \\ =\text{ 1970.444} \\ =\text{ 1970} \end{gathered}`

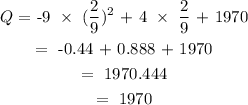
Final answer

The price which maximizes the total revenue is p = 2/9

The quantity is Q = 1970