Answer:
y = - 1
Step-by-step explanation:
Two lines are perpendicular if the product of their slopes is equal to -1.
Additionally, we can calculate the slope of a line with two points (x1, y1) and (x2, y2) as:

If we replace (x1, y1) by P(6, -2) and (x2, y2) by O(-2, 8), we get that the slope of PO is equal to:
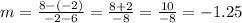
In the same way, if we replace (x1, y1) by (-4, 3) and (x2, y2) by (-9, y), we get that the slope of RS is equal to:
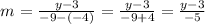
Then, the product of these two slopes should be equal to -1, so we can write the following equation:
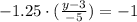
So, solving for y, we get:
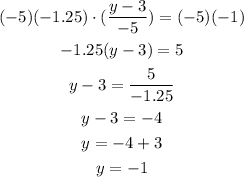
Therefore, the value of y is equal to -1