Given: Parallel lines PQ and RS. Triangle ABD and BDC are such that
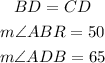
Required: To determine the triangle ABD type and calculate the angle BDC, ABD, and angle BAD.
Explanation: Since line PQ is parallel to line RS,
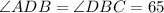
Now since BD=CD, triangle BCD is an isosceles triangle. Hence,
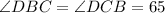
Now, in triangle BCD, we have

Now RS is a straight line. Hence at point B, we have
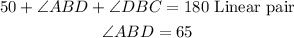
Finally, in triangle ABD, we have
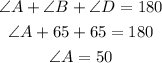
Now since in triangle ABD, we have
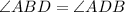
The triangle ABD is isosceles.
Final Answer:
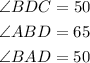
The triangle ABD is isosceles.