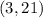Question

Find the coordinates of the other endpoint of the segment, given its midpoint and one endpoint. (Hint: Letmidpoint (2,9), endpoint (1, -3)

Answer 1

Given this is a one of the endpoints of the segment:

`(1,-3)`

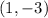
You know that the midpoint is:

`(2,9)`

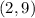
By definition, the formula for finding the midpoint of a segment is:

`(x_m,y_m)=((x_1+x_2)/(2),(y_1+y_2)/(2))`

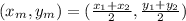
Where:

- The coordinates of the midpoint are:

`(x_m,y_m)`

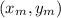
- And the coordinates of the endpoints are:

`\begin{gathered} (x_1,y_1) \\ (x_2,y_2) \end{gathered}`

In this case, you can set up that:

`\begin{gathered} x_m=2 \\ y_m=9 \\ \\ x_1=1 \\ y_1=-3 \end{gathered}`

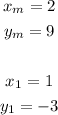
Then, you can set up this equation to find the x-coordinate of the other endpoint:

`2=(1+x_2)/(2)`

Solving for:

`x_2`

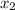
You get:

`(2)(2)=1+x_2`
`\begin{gathered} 4-1=x_2 \\ x_2=3 \end{gathered}`

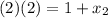
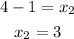
Set up the following equation to find the y-coordinate of the other endpoint:

`9=(-3+y_2)/(2)`
`(9)(2)=-3+y_2`
`\begin{gathered} 18+3=y_2 \\ y_2=21 \end{gathered}`

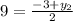
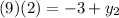
Hence, the answer is:

`(3,21)`