Answer:
Magnitude = 25.55 m
Angle = 30.58 degrees
Step-by-step explanation:
If the vector has the components Ax = 22 and Ay = 13, we can represent the vector as:
Therefore, the magnitude of this vector is the magnitude of the red vector. It means that we can calculate its length using the Pythagorean theorem where 22 and 13 are the legs, so:
![\sqrt[]{Ax^2+Ay^2}=\sqrt[]{22^2+13^2}=\sqrt[]{484+169}=\sqrt[]{653}=25.55\text{ m}](https://img.qammunity.org/2023/formulas/physics/college/z6pgwg21mh3cbwby6n3zsniu7ekiufvy8e.png)
Then, we can find the angle using the trigonometric function tangent, so:
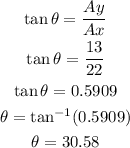
So, the answers are:
Magnitude = 25.55 m
Angle = 30.58 degrees