Question

Match each function with its graph 1. f (x) =x³+3x²2. f (x) = -x (x-1) (x+2)3. f (x) = -x³+3x²4. f (x) = x (x+1) (x-2)

Answer 1

to understand this graphs you must find the roots on each of the functions.

start by funtion 1.

`\begin{gathered} x^3+3x^2=0 \\ x\cdot(x^2+3x)=0 \\ x=0 \\ (x^2+3x)=0 \\ x(x+3)=0 \\ x=0 \\ x+3=0 \\ x=-3 \end{gathered}`

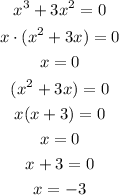
for function 1 you will need to find a graph that only intercept the x-axis on 0 an -3. In this case it will be the graph A.

Do the same for each function

`\begin{gathered} -x\cdot(x-1)\cdot(x+2) \\ x=0 \\ x-1=0 \\ x=1 \\ x+2=0 \\ x=-2 \end{gathered}`

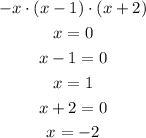
function 2, the interceptions are 0,1 and -2. Graph C will be the correct one for this function

function 3

`\begin{gathered} -x^3+3x^2=0 \\ x\cdot(-x^2+3x)=0 \\ x=0 \\ (-x^2+3x)=0 \\ x(-x+3)=0 \\ x=0 \\ -x+3=0 \\ x=3 \end{gathered}`

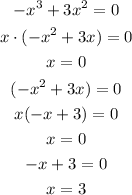
for fuction 3, roots will be 0 and 3, the associated graph will be D

and lastly the roots for function 4.

`\begin{gathered} -x\cdot(x+1)\cdot(x-2) \\ x=0 \\ x+1=0 \\ x=-1 \\ x-2=0 \\ x=2 \end{gathered}`

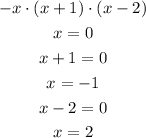
The associated graph is B.