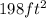Question

Find the area of the polygon. 17 ft 14 ft 4 ft- 3 ft 4 ft The area of the polygon is (Type a whole number.)

Answer 1

Notice that the polygon can be divided on 3 rectangles, as shown in the following diagram:

The 14 ft side on the original image was split on a segment of 10ft and another of 4ft.

The areas of these rectangles, are:

`\begin{gathered} A_1=(17ft)(10ft)=170ft^2 \\ A_2=(4ft)(3ft)=12ft^2 \\ A_3=(4ft)(4ft)=16ft^2 \end{gathered}`

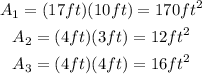
The total area of the polygon is the sum of the areas of the three rectangles:

`\begin{gathered} A=170ft^2+12ft^2+16ft^2 \\ =198ft^2 \end{gathered}`

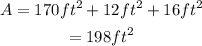
Therefore, the area of the polygon is:

`198ft^2`