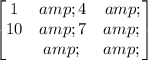The 2 x 2 matrix is given
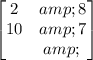
The row transformation given is:
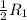
this means we take half of all the elements of Row 1
The process is shown below:
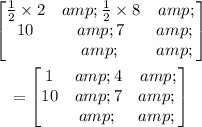
Hence, the final matrix Row 2 is same as previous matrix, but Row 1 is half of the elements of previous matrix.
Answer: