The equation of the regression line has the following shape:

Where m is calculated through the following equation:
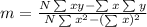
And b is calculated through the following equation:
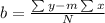
N is the number of samples. 8 for this case.
The values of all the sums present in the above equation are reported in the last row of the table:
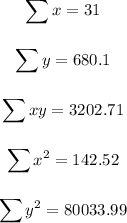
Now, we can begin calculating m by replacing the values:
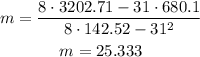
The slope of the equation is m = 25.333.
Now, we can calculate b:

Now that we know the parameters m and b for the linear regression, we can build the equation:
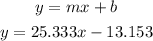
Where x represents the murders and y the robberies per 100,000 population.
Then, (a): the equation of the regression line is y = 25.333x - 13.153.
To predict the robberies per 100,000 population when x = 4.5 murders, we just need to replace that 4.5 in the equation that we just found:
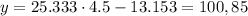
Finally, (b): according to the linear regression, the number of robberies per 100,000 population when x = 4.5 murders is approximately 100,85.