Question

5 Three pipes are connected to a water tank. One of the pipes can fill the tank in 30 minutes. The second pipe can fill it in 20 minutes. The third pipe can fill the tank in 40 minutes. How long will it take to fill the tank if all three pipes are opened together? If the slowest pipe is shut off after 3 minutes and the fastest pipe is shut off 3 minutes later, how long will it take the remaining open pipe to finish filling the tank?

Answer 1

Let's call the total volume of the tank as V. The rate each pipe fills the tank is given by the total volume of the tank divided by the amount of time it takes to fill the tank. Let's call the rate of the first pipe as r1, the rate of the second pipe as r2 and the rate of the third pipe as r3.

`\begin{gathered} r_1=(V)/(30) \\ r_2=(V)/(20) \\ r_3=(V)/(40) \end{gathered}`

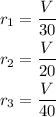
The product between the rate and the time that has passed will give to us the fraction of the tank that has been filled. When we open the three pipes at once, we sum their rates. When the tank is filled, the product between the rate and the time passed must give the total volume of the tank, therefore, we have the following equation:

`\begin{gathered} ((V)/(30)+(V)/(20)+(V)/(40))t=V \\ (13V)/(120)t=V \\ (13)/(120)t=1 \\ t=(120)/(13) \\ t=9.23076923077... \\ t\approx9.23 \end{gathered}`

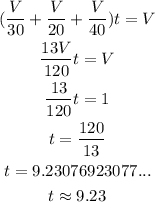
It will take approximately 9.23 minutes to fill the tank if all pipes are opened together.

When the three pipes are opened, the fraction that has been filled(let's call it as x) is given by:

`\begin{gathered} ((1)/(30)+(1)/(20)+(1)/(40))\cdot3=x \\ x=(13)/(40) \end{gathered}`

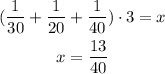
Then, the slowest pipe(the third pipe) is closed, then, after 3 more minutes we're going to fill an extra y amount of water, given by:

`\begin{gathered} ((1)/(30)+(1)/(20))\cdot3=y \\ (1)/(10)+(3)/(20)=y \\ (5)/(20)=y \\ y=(1)/(4) \end{gathered}`

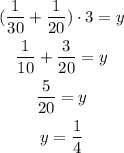
Then, after a time t with the first pipe open, we're going to fill the tank(remember that it has been filled already by the amounts x and y, therefore, we must subtract it from the total volume).

`\begin{gathered} (1)/(30)\cdot t=1-(13)/(40)-(1)/(4) \\ (t)/(30)=(27)/(40)-(10)/(40) \\ t=30\cdot(17)/(40) \\ t=12.75 \end{gathered}`

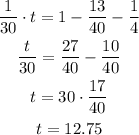
If the slowest pipe is shut off after 3 minutes and the fastest pipe is shut off 3 minutes later, it will take 12.75 minutes for the remaining open pipe to finish filling the tank.