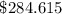Given that:
- Cory saves $30 in June.
- Each month he plans to save 10% more than the previous month.
- He saves money from June to December.
You can convert 10% to a decimal number by dividing it by 100:
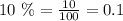
You already know that he has $30 in June. Then, you can determine that the amount of money (in dollars) he will save in July is:
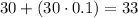
By definition, the formula for the Sum of a Geometric Sequence is:
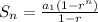
Where "r" is the Common Ratio, "n" is the number of terms, and this is the first term:
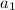
In this case, you can identify that the first term is:
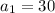
And the second term is:

Therefore, you can find the Common Ratio as follows:
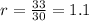
Since he saves money from June to December, the sequence has 7 terms. Then:
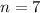
Now you can substitute values into the formula and evaluate:

Hence, the answer is: