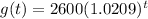The population at the beginning of 1950 was 2600 thousand people.
Then it started increasing exponentially 23% every decade.
The general form of any exponential function is:
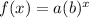
Where
a is the initial value
b is the growth/decay factor
x is the number of time periods
y is the final value after x time periods
a. To calculate the growth factor of an exponential function, you have to add the increase rate (expressed as a decimal value) to 1:
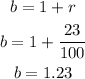
b. Considering the initial value a= 2600 thousand people and the growth factor b=1.23, you can express the exponential function in terms of the number of decades, d, as follows:
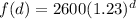
c. Considering that the time unit is measured in decades, i.e d=1 represents 10 years
To determine the corresponding value of the variable d for 1 year, you have to divide 1 by 10
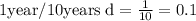
Calculate the growth factor powered by 0.1:
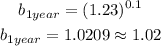
d. Use the factor calculated in item c