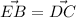Construction: Join ED.
The corresponding diagram is given below,
According to the given problem,
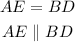
Since a pair of opposite sides are parallel and equal, it can be claimed that quadrilateral ABDE is a parallelogram.
Then, as a property of any parallelogram, it can be argued that,
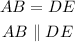
Given that B is the mid-point of AC,
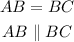
Combining the above two results,
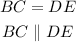
It follows that ABCD also forms a parallelogram.
Again using the property that opposite sides of a parallelogram are equal and parallel. It can be claimed that,
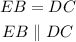
Hence proved that segment EB is parallel to segment DC,