Question

Which function has the following characteristics? • A vertical asymptote at x = 3 • A horizontal asymptote at y = 2 Domain: {** +3] 2x - 8 X - 3 y=x2-9 2 9 x² - 4 4 OB. V C. 2x2 - 18 x² - 4 4 2x2 - 8 O D. ** - 9

Answer 1

To get this, note that the vertical asymptote can be gotten by setting the denominator to be equal to 0.

If we do this, we will notice that the vertical asymptote of option A and option D is x = 3

That is

for option A

`\begin{gathered} y=(2x-8)/(x-3) \\ x-3=0 \\ x=3 \end{gathered}`

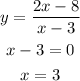
For option D

`\begin{gathered} y=(2x^2-8)/(x^2-9) \\ x^2-9=0 \\ x^2=9 \\ x=3 \end{gathered}`

So, the answer is either option A or D.

But to get the correct answer, let us look at the graphs for both functions

Graph of A

`y=(2x-8)/(x-3)`

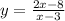
From the graph, you can see that the domain is defined at x = 3. Notice that the green line cut across x = 3.

Now let's check Graph of option D

`y=(2x^2-8)/(x^2-9)`

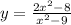
From the graph, you can see that the domain is defined at x = -3 and x = 3. Notice that the purple and green line cut across x = -3 and x = 3. So, the domain here is

`x=\pm3`

Hence