Here, we want to graph the part of the graph that is one-to-one
What we have to do here is to remove the absolute value signs and plot the graph of the line that it normally looks like
Generally, we have the equation of a straight line as;
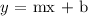
where m is the slope and b is the y-intercept
Looking at the function f(x) = 2x-4; -4 is simply the y-intercept value
So, we have a point at (0,-4)
To get the second point, set f(x) = 0
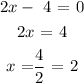
So, we have the second point as (2,0)
By joining (2,0) to (0,-4) ; we have the plot of the part of the function that extends to infinity