Question

Write the slope-intercept form of the equation of the line describedthrough: (-5, 4), perp. to y=3/4x+4

Answer 1

To find the equation of the line passes through (-5,4) and perpendicular to the line y=3/4 x +4

The slope of the line y=3x/4 +4 is 3/4

Let m be the slope of the required equation of the line,

Since these two lines are perpendicular to each other.

we know that,

Product of the slopes of the perpendicular lines is -1

That is,

`(3)/(4)* m=-1`

`m=-(4)/(3)`

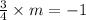
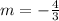
Slope of the required line is -4/3

Passes through the point (-5,4)

The equation of the line passes through the point (x1,y1) and m as its slope is

`(y-y1)=m(x-x1)`

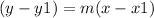
Substitute x1=-5, y1=4 and m=-4/3

we get,

`(y-4)=-(4)/(3)(x+5)`

`y-4=-(4)/(3)x-(20)/(3)`

`y=-(4)/(3)x-(20)/(3)+4`

`y=-(4)/(3)x+((-20)+12)/(3)`

`y=-(4)/(3)x-(8)/(3)`

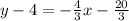
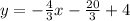
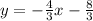
The required slope-intercept form of the equation of the line is y=-4/3 x-8/3.