Given,
The equations are
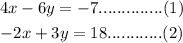
To find: Does the following system have a unique solution? Why?
Solution:
The determinant of the given equations are
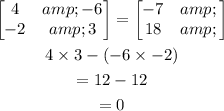
For unique solutions, the condition is

Condition satisfied.
Hence, the given equations have a unique solution.