Question

How much you learned about the inverse, converse, and contrapositive of a conditional (if-then) statement, and how this can be applied in real life

Answer 1

A conditional statement can be written as:

`p\rightarrow q`

An example of this in real life is:

`\text{If it rains then the floor gets wet.}`

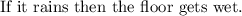
In this case:

p = it rains

q = the floor gets wet

The converse of that conditional is:

`\begin{gathered} q\rightarrow p \\ \text{If the floor gets wet then it rains.} \end{gathered}`

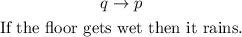
Notice that the conditional being true doesn't mean necessarily that its converse is true. For example, every time it rains the floor gets wet can be true, but the floor could get wet for other reasons, so the converse would not be true.

Also, the inverse of that conditional is:

`\begin{gathered} \\eg p\rightarrow\\eg q \\ \text{If it does not rain then the floor does not get wet.} \end{gathered}`

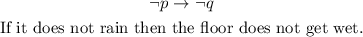
As we see, the inverse of a true conditional statement is not necessarily true.

And the contrapositive of that conditional statement is:

`\begin{gathered} \\eg q\rightarrow\\eg p \\ \text{If the floor does not get wet then it does not rain.} \end{gathered}`

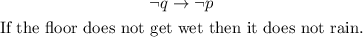
Now, the contrapositive of a true conditional statement is always true. Notice that if every time it rains the floor gets wet, the only explanation for the floor not getting wet is that it does not rain.