Answer
Step-by-step explanation
Given:
A spherical balloon is inflated with gas at the rate of 800 cubic centimeters per minute means
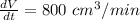
(a) The rates of change of the radius when r = 30 centimeters and r = 85 centimeters is calculated as follows:
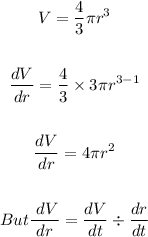
So when r = 30, we have

Therefore, the rate of change of the radius when r = 30 is dr/dt = 0.071 cm/min.
For when r = 25 cm, the rate of change is:
