The average height is μ= 5.9ft and has a standard deviation of σ=0.2ft.
You have to determine the height (X) for the Z-score z=2
To determine this value, you have to use the formula of the standard deviation:
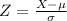
First, write the equation for X:
-Multiply both sides by sigma:
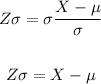
-Add mu to both sides of it:
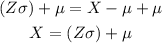
Replace the expression obtained for X with the known values of z, sigma, and mu
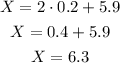
The height of a man that corresponds to z=2 is 6.3 ft