So first of all we need to write an algebraic equation for Mike. We know that he bought 3 coffees and 1 doughnut. Then the total price of these things is:
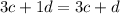
And we know that he had to pay $19 so this expression is equal to 19:
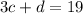
Then the answer to question 14 is the second option.
Bob bought one coffee and one doughnut so the total cost of his purchase is:
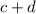
We know that this cost is equal to $9 so we get:
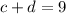
And the answer to question 15 is the third option.
In question2 16 and 17 we need to find c and d. For this purpose we need to use the algebraic equations for Mike and Bob:
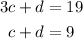
Let's take the second equation and substract c from both sides:
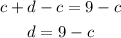
Now we substitute this expression in place of d in the first equation:
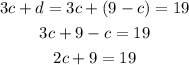
Now we substract 9 from both sides:
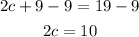
And we divide both sides by 2:
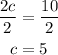
Then the price of one coffee is $5 so the answer to question 16 is the third option.
Now we are going to take the equation for Bob and take c=5:
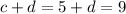
If we substract 5 from both sides we get:
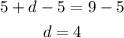
Then the price of one doughnut is $4 and the answer to question 17 is the second option.