Question

find the sum of the first 6 terms of the following sequence. round to the nearest hundredth if necessary.35, 14, 28/5,...sum of a finite geometric series:Sn=a1-a1^r^n/1-r

Answer 1

58.09

Step-by-step explanation

To find the sum of a finite geometric series, use the formula,

`S_n=(a(1-r^n))/((1-r))`

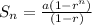
where

`\begin{gathered} a=\text{ first term} \\ r=\text{ common ratio} \\ n=\text{ number of terms} \\ S_n=sumo\text{f the firts n terms} \end{gathered}`

so

Step 1

find the common ratio :

To calculate the common ratio in a geometric sequence, divide the n^th term by the (n - 1)^th term,in other words you can just divide each number from the number preceding it in the sequence

`coomin\text{ ratio =}\frac{n\text{ term }}{(n-1)\text{ term}}`

so

`common\text{ ratio=}((28)/(5))/((14)/(1))=(28)/(70)=0.4`

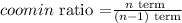
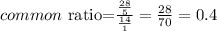
so r= 0.4

Step 2

Now we can use the formula

a)

let

`\begin{gathered} r=0.4 \\ n=\text{ 6} \\ a=35 \end{gathered}`

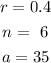
b) finally, replace in the formula

`\begin{gathered} S_n=(a(1-r^n))/((1-r)) \\ S_n=(35(1-0.4^6))/((1-0.4)) \\ Sn=35*1.62984 \\ Sn=58.0944\text{ } \\ rounded \\ S_n=58.09 \end{gathered}`

therefore, the answer is

58.09

I hope this helps you