Question

a) How many hand-held color televisions can be sold at $ 400 per television?b) How many televisions will be sold when supply and demand are equal?c) Find the price at which supply and demand are equal.

Answer 1

a) Since we are interested in the number of TVs that can be sold at $400, we need to use the Demand model equation and set p=400; thus,

`\begin{gathered} p=400 \\ \Rightarrow N=-7\cdot400+2820=20 \\ \Rightarrow N=20 \end{gathered}`

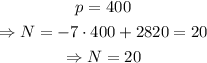
The answer to part a) is 20 TVs per week.

b) Set N=N, then

`\begin{gathered} N=N \\ \Rightarrow-7p+2820=2.4p \\ \Rightarrow9.4p=2820 \\ \Rightarrow p=(2820)/(9.4)=300 \\ \Rightarrow p=300 \end{gathered}`

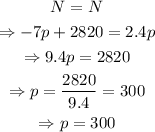
Therefore, using p=300 and solving for N,

`\begin{gathered} \Rightarrow N=2.4\cdot300=720 \\ \Rightarrow N=720 \end{gathered}`

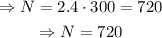
The answer to part b) is 720 TVs per week.

c) In part b), we found that when supply and demand are equal, p=300. Thus, the answer to part c) is $300