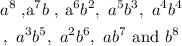Step-by-step explanation:
Remember the Binomial Theorem:
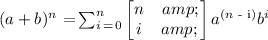
Now, consider the following polynomial:
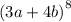
Applying the Binomial Theorem, where:
a = 3a
b= 4b
we get:
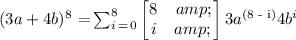
thus, expanding the sum, we get:
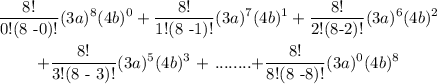
Now, simplifying we get:
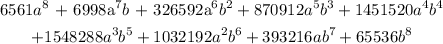
then, we can conclude that the correct answer is:
Answer:
The variable terms are: