ANSWER
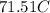
Step-by-step explanation
Parameters given:
Mass of thermometer, m = 300 g
Initial temperature of thermometer, t1 = 35°C
Volume of water, V = 258 cm³
Initial temperature of water, T1 = 80°C
First, let us find the mass of the water using the formula for density:
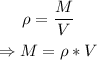
where ρ = density of water = 1 g/cm³
Therefore, the mass of the water is:
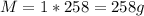
According to the conservation of energy, the total heat flow (the sum of the heat energy of the thermometer and water) must be equal to 0 since no heat flows to the surroundings:
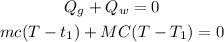
where c = specific heat capacity of glass thermometer = 0.2 cal/g°C
C = specific heat capacity of water = 1 cal/g°C
T = final temperature of thermometer and water
Hence, solving for T, we have that:

That is the final temperature of the thermometer.