Question

F(x) =2x^2+12x-6 Does this function have a minimum or maximum value? What is this minimum or maximum value?

Answer 1

Let's compare the given function with the model for a quadratic equation:

`\begin{gathered} f(x)=ax^2+bx+b \\ a=2,b=12,c=-6 \end{gathered}`

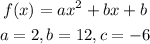
Since the value of a is positive, the parabola has its concavity upwards, and the function has a minimum value.

The minimum value can be found calculating the y-coordinate of the vertex:

`\begin{gathered} x_v=-(b)/(2a)=-(12)/(4)=-3 \\ \\ y_v=2\cdot(-3)^2+12\cdot(-3)-6 \\ y_v=2\cdot9-36-6^{} \\ y_v=-24 \end{gathered}`

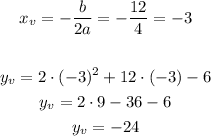
Therefore the minimum value is -24.