Question

mean is 95.3standard deviation is 15.4 finf the probability that a randomly selected adult IQ is greater than 119.8

Answer 1

we are asked to determine the probability that a variable x is greater than 119.8. To do that we will assume a normal distribution of probability and use the following relationship:

`P(x>119.8)=1-P(x\le119.8)`

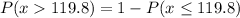
To determine the probability that x is smaller than 119.8 we need first to find the z-score of the data set using the following formula:

`z=\frac{x-\bar{x}}{\sigma}`

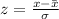
Where

replacing we get:

`z=(119.8-95.3)/(15.4)=1.59`

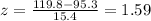
Now we use this value to look into the chart for probabilities, we get 0.94408. This is the probability that x is smaller than 119.8. Replacing in the initial relationship we get:

`P(x>119.8)=1-0.94408=0.056`

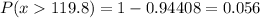
Therefore, the probability is 5.6%.