Question

This is non graded algebra 1 I need help on question 10

Answer 1

An exponential decay function can be generically written as:

`y=a\cdot b^x`

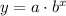
The conditions for this function are:

1) The y-intercept is 4.

2) The values of y decrease by a factor of one half as x increases by 1.

The y-intercept corresponds to the value of y when x = 0, so we can express it as:

`\begin{gathered} y=a\cdot b^x \\ 4=a\cdot b^0 \\ 4=a\cdot1 \\ a=4 \end{gathered}`

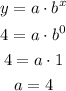
This condition let us find the value of a.

The next condition will be used to find the value of b.

As x increases by 1, y decreases by one half.

We can write this as a quotient between consecutive values of y:

`\begin{gathered} (y(x+1))/(y(x))=(1)/(2) \\ (4\cdot b^(x+1))/(4\cdot b^x)=(1)/(2) \\ b^(x+1-x)=(1)/(2) \\ b^1=(1)/(2) \\ b=(1)/(2) \end{gathered}`

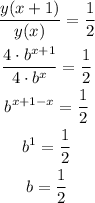
Then, we can write the function as:

`y=4\cdot((1)/(2))^x`

Answer: y = 4*(1/2)^x