Question

Pls help: find the rational expression state any restrictions on the variable

Answer 1

Simplification of Rational Expressions

Given the rational expression:

`(n^4-10n^2+24)/(n^4-9n^2+18)`

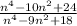
Simplify and state the restriction for the variable n.

Let's work on the numerator and denominator independently. Factoring the numerator:

`\begin{gathered} n^4-10n^2+24=n^4-4n^2-6n^2+24 \\ n^4-10n^2+24=n^2(n^2-4)-6(n^2-4) \\ n^4-10n^2+24=(n^2-6)\mleft(n^2-4\mright) \end{gathered}`

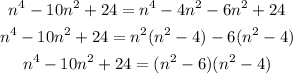
The denominator can be factored in a similar way:

`\begin{gathered} n^4-9n^2+18=n^4-3n^2-6n^2+18 \\ n^4-9n^2+18=n^2(n^2-3)-6(n^2-3) \\ n^4-9n^2+18=\mleft(n^2-3\mright)(n^2-6) \end{gathered}`

Thus, rewriting the expression:

`(n^4-10n^2+24)/(n^4-9n^2+18)=((n^2-4)(n^2-6))/((n^2-3)(n^2-6))`

Before simplifying, we must state the restrictions for the variable. The denominator cannot be 0, thus:

`\begin{gathered} n^2-3\\e0\Rightarrow n\\e\pm\sqrt[]{3} \\ n^2-6\\e0\Rightarrow n\\e\pm\sqrt[]{6} \end{gathered}`

Now simplify:

`(n^4-10n^2+24)/(n^4-9n^2+18)=((n^2-4))/((n^2-3))`

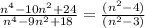
Combining the final expression with the restrictions, we stick with choice a.