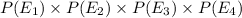Answer:
The probability of having all four events is;
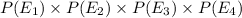
Step-by-step explanation:
Given that there are four independent events E1,E2,E3 and E4.
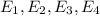
The probability of having all the four events;
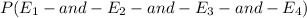
would be the product of the probability of each of the events;
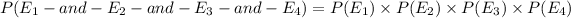
Therefore, the probability of having all the four events is;