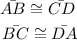Given that ABCD is a parallelogram, prove that
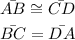
step 1: Sketch the parallelogram
step 2: The diagonal AC, divides the parallelogram into two triangles

step 3: By the ASA (Angle-Side-Angle) congruency theorem,
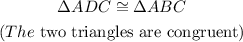
Hence, by CPCT (corresponding parts of congruent triangles)