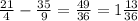Question

2 2 3 4 5 Enter an estimate. Round each mixed number to the nearest whole in your estimate. -38 4 9 Estimate: Find the difference and enter it in simplest form. 3 60

Answer 1

`5(1)/(4)-3(8)/(9)`

To make the estimate of the substraction of the mixed numbers we use the fraction that is accompaning the whole number. If the number is less than 1/2 we say that the number is closer to the whole number before the fraction, if it is 1/2 or more then we add one to the whole number.

For the first number

`5(1)/(4)\approx5`

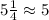
This is approximate to 5 because 1/4 is less than 1/2

For the second number

`3(8)/(9)\approx4`

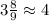
This is approximate to 4 because 8/9 is greater than 1/2.

ESTIMATE

`\begin{gathered} 5(1)/(4)-3(8)/(9)=\text{?} \\ 5-4\approx1 \end{gathered}`

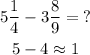
To pass a mixed number into a fraction we use the following procedure

`a(b)/(c)=((a\cdot c)+b)/(c)`

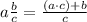
Pass both mixed numbers

`\begin{gathered} 5(1)/(4)=((5\cdot4)+1)/(4)=(20+1)/(4)=(21)/(4) \\ 3(8)/(9)=((3\cdot9)+8)/(9)=(27+8)/(9)=(35)/(9) \end{gathered}`

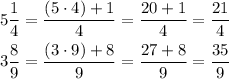
To find the exact value

`(21)/(4)-(35)/(9)=(21\cdot9-35\cdot4)/(9\cdot4)=(49)/(36)`

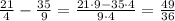
answer

The exact value of the substraction is

`(21)/(4)-(35)/(9)=(49)/(36)=1(13)/(36)`