Question

Hi! Can someone please check my work real quick? I’m not sure what I’m doing wrong. I’m trying fo find the remainder using synthetic division.

Answer 1

Given:

The polynomial is given as,

`\begin{gathered} p(x)=2x^3+4x^2-5 \\ g(x)=x+3 \end{gathered}`

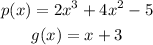
The objective is to divide the polynomial by synthetic division.

Step-by-step explanation:

The general equation of a polynomial with degree 3 is,

`f(x)=ax^3+bx^2+cx+d`

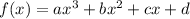
So, consider the given polynomial as,

`p(x)=2x^3+4x^2+0x-5`

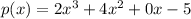
The divisor can be converted as,

`\begin{gathered} x+3=0 \\ x=-3 \end{gathered}`

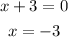
To find synthetic division:

Now, the synthetic division can be evaluated as,

Hence, the remainder of the division is -23.