Question

The organizer of a conference is selecting workshops to include. She will select from 6 workshops about chemistry and 7 workshops about biology. In how many ways can she select 4 workshops if 2 or fewer must be about chemistry?

Answer 1

Given that there are 6 workshops about chemistry and 7 workshops about biology.

So the total number of workshops available are,

`\begin{gathered} =6+7 \\ =13 \end{gathered}`

The number of ways of selecting 'r' objects from 'n' distinct objects is given by,

`^nC_r=(n!)/(r!\cdot(n-r)!)`

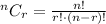
The total number of ways of selecting 4 workshops having no workshop about chemistry is calculated as,

`\begin{gathered} n(\text{ 0 chemistry)}=^7C_4 \\ n(\text{ 0 chemistry)}=(7!)/(4!\cdot(7-4)!) \\ n(\text{ 0 chemistry)}=(7\cdot6\cdot5\cdot4!)/(4!\cdot3!) \\ n(\text{ 0 chemistry)}=(7\cdot6\cdot5)/(3\cdot2\cdot1) \\ n(\text{ 0 chemistry)}=35 \end{gathered}`

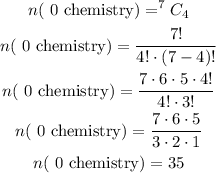
The total number of ways of selecting 4 workshops having exactly 1 workshop about chemistry is calculated as,

`\begin{gathered} n(\text{ 1 chemistry)}=^7C_3\cdot^6C_1 \\ n(\text{ 1 chemistry)}=(7!)/(3!\cdot(7-3)!)\cdot(6!)/(1!\cdot(6-1)!) \\ n(\text{ 1 chemistry)}=(7\cdot6\cdot5\cdot4\cdot3!)/(3!\cdot4!)\cdot(6\cdot5!)/(1!\cdot5!) \\ n(\text{ 1 chemistry)}=(7\cdot6\cdot5\cdot4)/(4\cdot3\cdot2\cdot1)\cdot6 \\ n(\text{ 1 chemistry)}=210 \end{gathered}`

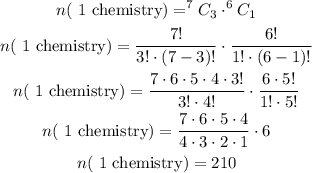
The total number of ways of selecting 4 workshops having exactly 2 workshops about chemistry is calculated as,

`\begin{gathered} n(\text{ 2 chemistry)}=^7C_2\cdot^6C_2 \\ n(\text{ 2 chemistry)}=(7!)/(2!\cdot(7-2)!)\cdot(6!)/(2!\cdot(6-2)!) \\ n(\text{ 2 chemistry)}=(7\cdot6\cdot5!)/(2!\cdot5!)\cdot(6\cdot5\cdot4!)/(2!\cdot4!) \\ n(\text{ 2 chemistry)}=(7\cdot6)/(2\cdot1)\cdot(6\cdot5)/(2\cdot1) \\ n(\text{ 2 chemistry)}=315 \end{gathered}`

Consider that the number of ways to select 4 workshops if 2 or fewer must be about chemistry, will be equal to the sum of the individual cases when the number of chemistry workshops in the selection are either 0 or 1 or 2.

This can be calculated as follows,

`\begin{gathered} \text{ Total}=n(\text{ 0 chemistry)}+n(\text{ 1 chemistry)}+n(\text{ 2 chemistry)} \\ \text{Total}=35+210+315 \\ \text{Total}=560 \end{gathered}`

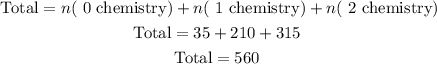
Thus, the total number of ways is 560.