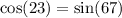Question

JUST NEED HELP ON THE LAST ONE AND A VERIFICATION ON EVERYTHING ELSE !!!!!!!!!

Answer 1

In any right triangle with acute angles x and y, then

The sum of x and y is 90 degrees

`\begin{gathered} \sin x=\cos y \\ \cos x=\sin y \\ x+y=90^(\circ) \end{gathered}`

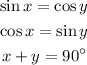
Then for part (1)

Since triangle XYZ is a right angle at Z

Then

`X+Y=90^(\circ)`

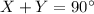
Then X and Y are complementary angles

Part (2)

sin X = opposite/hypotenuse

`\sin X=(x)/(z)`

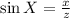
sin Y = opposite/hypotenuse

`\sin Y=(y)/(z)`

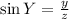
cos X = adjacent/hypotenuse

`\cos X=(y)/(z)`

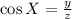
cos Y = adjacent/hypotenuse

`\cos Y=(x)/(z)`

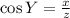
Part (3)

`\begin{gathered} \sin X=\cos Y \\ \cos X=\sin Y \end{gathered}`

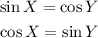
Part (4)

Since sin = cos, then

The sum of the 2 angles must be 90

One of them is 23 degrees, then the other must be

`90-23=67`

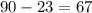
The answer is

`\cos (23)=\sin (67)`