We are given the following expression:
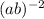
First, we will use the following property of exponentials:
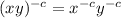
Applying the property we get:
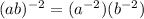
Now, we use the following property of exponentials:
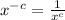
Applying the property we get:
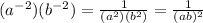
Since we can't simplify any further this is the final answer.