The information we have is:
Mean:
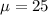
Standard deviation:
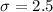
Value of x:
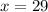
--------------------------------------------------------
To solve this problem, we need to use the z-score formula:
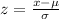
Substituting our values:
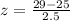
We need to solve the subtraction first:
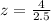
Finally, solve the division to find the z-score:
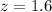
the z-score is 1.6
Answer: 1.6