Answer:
Using point (-21, -22): y = (6/7)x - 4
Using point (-14, -16): y = (6/7)x - 4
Step-by-step explanation:
The point-slope form of a line's equation is:

Where (x₁, y₁) is a point in the line and m is the slope.
The slope of a line can be calculated as:

Where (x₁, y₁) and (x₂, y₂) are two points in the line. So, replacing (x₁, y₁) by (-21, -22) and (x₂, y₂) by (-14, -16), we get that the slope of the line is:
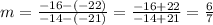
Now, using the point (-21, -22), we get that the equation of the line is:
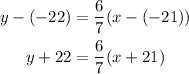
Then, we can simplify the equation as:
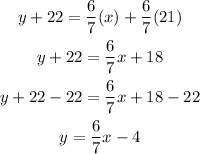
On the other hand, using the point (-14, -16), the equation of the line is:
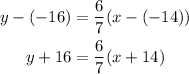
Simplifying, we get:
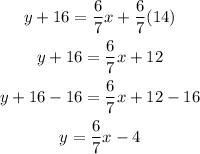
So, the answers are:
Using point (-21, -22): y = (6/7)x - 4
Using point (-14, -16): y = (6/7)x - 4