Given:
BC = 3 cm, FG = 4 cm
Required: bLength of EF and ratio of areas
Step-by-step explanation:
(a) Since the rectangles ABCD and EFGH are similar, the correponding angles are proportional. Hence
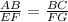
Plug the given values.
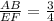
If AB = a cm, then
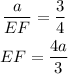
(b) Ara of ABCD

Area of EFGH
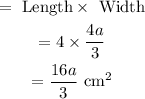
Ratio of areas
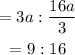
Final Answer: The ratio of areas of ABCD to EFGH is 916.