It is required to find the number of ways 6 different students can be arranged.
Since the students are different and they are required to be arranged in a line, the number of ways is:
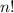
Where n is the number of items.
Hence, for 6 students the number of ways of arranging them on a line is:
![6!=6\cdot5\operatorname{\cdot}4\operatorname{\cdot}3\operatorname{\cdot}2\operatorname{\cdot}1=720\text{ ways}]()
The answer is 720 ways.