The straight line equation is

where m is the slope and b the y-intercept. In our case m=-9. Hence, our line
equations has the form
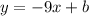
In order to find b, we must use the given point (-4,-2) and substitute it and the last equation.
It yields,

hence, we have
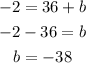
Finally, the answer is

Now, we can rewrite this equation as
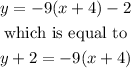
then, the answer is C.