Question

An object is placed 10.0 cm in front of a thin concave lens with a focal length of 18 cm. Calculate the imageposition

Answer 1

The focal length of a concave lens is expressed as,

`(1)/(f)=(1)/(u)+(1)/(v)`

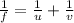
Here, f is the focal length, u is the distance of object and v is the distance of image.

Plug in the known values,

`\begin{gathered} \frac{1}{18\text{ cm}}=\frac{1}{10.0\text{ cm}}+(1)/(v) \\ (1)/(v)=\frac{1}{18\text{ cm}}-\frac{1}{10.0\text{ cm}} \\ v=\frac{(18\text{ cm)(10.0 cm)}}{10.0\text{ cm-18 cm}} \\ =-22.5\text{ cm} \end{gathered}`

Thus, the distance of image is -22.5 cm where negative sign indicates that the image will be at the same side of object.