Question

Brad expects that he will need $12,000 in 6 years to start an engineering consulting business. He has been offered an investment at 5%, compounded monthly. How much must he invest today to have enough money in 6 years? How much interest will he have earned?

Answer 1

Invest today: $8895.36

Interest earned: $3104.64

Step-by-step explanation:

The amount after t years can be calculated as:

`A=P(1+(r)/(n))^(nt)`

Where P is the initial amount invested, r is the interest rate and t is the number of years and n is the number of times the interest rate is compound. Solving the equation for P, we get:

`P=(A)/((1+(r)/(n))^(nt))`

Now, we can replace A by $12,000, r by 5% = 0.05, n by 12 because it is compounded monthly and t by 6

`P=(12000)/((1+(0.05)/(12))^(12(6)))=8895.36`

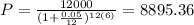
Therefore, he should invest $8895.36 today to have enough money in 6 years.

Finally, the interest earned is calculated as

$12000 - $8895.36 = $3104.64

So, the answers are:

Invest today: $8895.36

Interest earned: $3104.64