The given equation is:
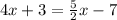
Solve the equation for x:

Next substitute the solution into each equation.
The equation that the solution satisfies is equivalent to the original equation.
Check for the first equation:

Since the solution does not satisfy the equation, it follows that the equation is not equivalent to the original equation.
Hence, select NO for the first equation.
Use the same procedure to check for the other equations.
Only the third and fourth equations are equivalent to the original equation, so feel yes for them, but no for the first and second.