Question

Options for the first box: inverse and direct Options: 275, 50, 5,000, 13,750 Options for the third box: $275.00, $137.50, $550.00

Answer 1

Answer:

• The proportional situation represents an Inverse Variation

,

• The constant of variation, k = 13750

,

• If all 100 students participate in the fundraiser, each will contribute $137.5

Step-by-step explanation:

From the given information, we notice that the more students involved in the fundraiser, the less the amount each student needs to contribute.

This is an INVERSE VARIATION

Let s represent the number of students who participated in the fundraiser, and t represents the amount needed to be contributed by each student, we have:

`\begin{gathered} s\propto(1)/(t) \\ \\ \Rightarrow s=(k)/(t) \\ \\ OR \\ st=k \end{gathered}`

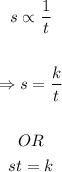
To find k, we use the information that s = 50 when t = 275

So,

`\begin{gathered} k=50*275 \\ =13750 \end{gathered}`

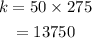
From the above, we have the formula:

`st=13750`

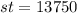
If 100 students participate in the fundraiser, we have:

`\begin{gathered} 100t=13750 \\ t=(13750)/(100)=137.5 \end{gathered}`

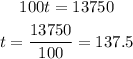
Each student needs to contribute $137.5