Answer:
P(Overbooking) = 0.0898
P(Empty seats) = 0.7461
Step-by-step explanation:
The probability that overbooking occurs is the probability that arrives more than 6 passengers from the 9 that remain.
This probability can be calculated as:

Where n is the total number of remaining passengers, and p is the probability that a passenger will arrive for the flight. So, the probability that x people arrive is:
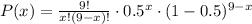
So, the probability that arrives 7, 8, or 9 people is:
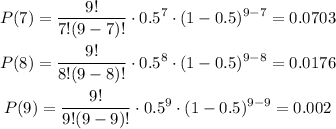
Therefore, the probability that overbooking occurs is:
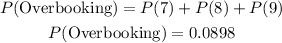
On the other hand, the probability that the flight has empty seats is the probability that arrives fewer than 6 people for the flight.
So, using the same equation for P(x), we get that the probability that the flight has empty sats is:

Therefore, the answers are:
P(Overbooking) = 0.0898
P(Empty seats) = 0.7461